Minimizing KL divergences
| Date | 2007-07-03 |
The following material is probably well known by specialists, but it gives good insights.
Suppose you have a true complex distribution $p$ and you want to approximate it by a simpler one, $q$, belonging to a family $F$ of easy distributions, say $F$= set of all gaussians. A common approach is to find the $q$ in $F$ which minimizes the $\text{KL}$ divergence between $p$ and $q$. Two possibilities arise, since the $\text{KL}$ is not symmetric :
- Minimizing $\text{KL}(q,p)$ — called exclusive or zero-forcing
- Minimizing $\text{KL}(p,q)$ — called inclusive or zero-avoiding
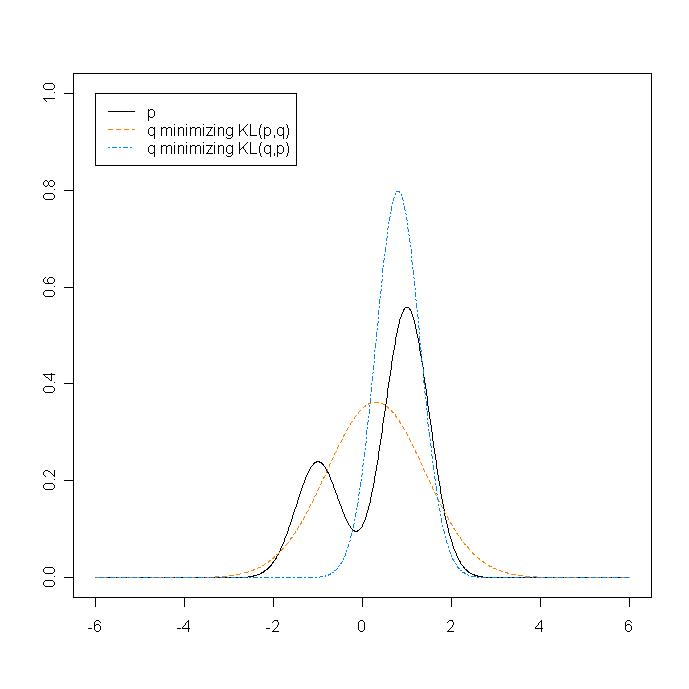
Why those names?
- $\text{KL}(q,p)$ : in this case $p(x)=0 => q(x)=0$ : zero-forcing.
Moreover, $q$ focuses on the biggest mode of $p$ , thus underestimates the variance of $p$. It is exclusive, it excludes some part of $p$. Some variational methods like Mean-field are approximations based on this minimization, and it’s known that the resulting is often over-confident (too small variance). But this can be an advantage, it depends on the model and problem. For instance, in mixture models, the posterior is polluted with replicated modes due to some symmetries in the model (ie labellings of the mixture components). Then $\text{KL}(q,p)$ will focus on just one mode, which is a good thing.
- $\text{KL}(p,q)$ : $p(x)>0 => q(x)>0$ : zero-avoiding.
The resulting $q$ will try to “cover all the p“. This can be bad if $p$ has 2 equals but distant modes, by putting a lot of mass in the middle of nowhere. A good thing with $\text{KL}(p,q)$ is that, if x is a n-dimensional vector, and if F is a family of fully factorized distributions, then the marginals of $q$ are exactly the marginals of $p$. Traditional Expectation Propagation is based on $\text{KL}(p,q)$. Another good point is that, if F is an exponential family, then the minimization is really easy : it’s just computing the moments of $p$ and choosing the $q$ in F with those moments.
Source and details : Minka’s paper
Comments
Very nice posting! I could never understand the D(approximation |truth) approach, because it is so easier to get silly results as one controls how the logarithmic loss gets integrated over the whole space of potential outcomes, but this description does provide an interesting rationale.
Comment by Aleks — July 9, 2007
[…] Yet Another Machine Learning Blog » Minimizing KL divergences [Pierre Dangauthier] (tags: KL) […]
Pingback by links for 2007-11-07 « 笨愚斋 — November 7, 2007