A Formal definition of intelligence
| Date | 2007-06-06 |
Shane Legg and Marcus Hutter recently introduced a formal, non-anthropocentric and general definition of intelligence. It is not based on any comparison with man/animals but it has its foundations in information and computation theory.
The intelligence $\gamma$ of an agent $\pi$ is:
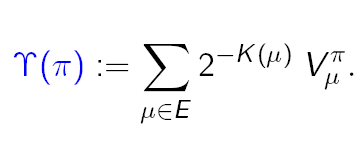
Where $\mu$ ranges over all possible environments (E), $(2^-K(\mu))$ is the probability of the environment $\mu$ and (V^pi_mu) measures the performance of the agent $\pi$ in the particular environment $\mu$.
Intuitively, this formula transcripts the following hypotheses :
- “Intelligence measures an individual’s general ability to succeed in a range of environments“
- success can be modeled by expected future reward in a reinforcement-learning ontology of the agent-environment interactions
- intelligence is the weighted average of success over the set of all possible environments
- the probability of a given environment is function of its Kolmogorov complexity (universal prior).
The interested reader can have a look at this short pdf presentation for more details.
This definition seems to have some good qualities, and I like a lot the idea of non-anthropocentricity. It doesn’t depend on any analogy with human intelligence (except the 1st of the preceding hypotheses). However some things are not so clear for me:
- The use of the universal prior, coming from Hutter’s approach (universal bayesianism). Does the choice of a Turing machine changes a lot the probabilities? Does it just influence the normalization constant. (I’m not familiar with this)
- Why should a more complex environment be less probable? It’s seems that a particular agent will face different env. with a non-universal probability, depending on its location, time… For instance, a cat isn’t likely to live in the empty intergalaxical space, even if it’s a really simple environment. Is this kind of context encodable by the choice of the Turing machine, does the choice of the Turing machine is a subjective prior?
- the reinforcement learning model describes the environment as a probability $p(\text{observation}, \text{reward}\ | \text{history})$. Is it a subjective probability?
- if yes : who is the subject? the agent? ahh nested stuff..
- if no : is it the same semantics as the universal prior?
- Another remark is the practical usefulness of such a definition. How to compute it? Summing over all environments? Computation of the Kol. complexity? And also the expected reward is intractable, especially in real life where nobody knows the future of any environment. This definition, and the associated fields of Kol. complexity, Solomonoff induction, computational learning theory, seems quite far from a (robotic) implementation, but are philosophically really appealing.
Could I risk a ladder of theory to practice among probabilist-AI approaches ?
- computational learning theory
- learning theory (exotic bounds)
- objectiveBayes (non informative or reference improper priors)
- subjectiveBayes (does anyone have ever written down a real-complete-honest subjective prior?)
- learning theory (kernel methods and boosting)
- frequenceProba (estimators, tests and regressions)
- quick bayes (spam filtering, robotics…)
Comments
This seems to circumvent the real problem of defining intelligence, which is how to measure performance in a meaningful way. In fact, maybe this formalism is a step backwards, because now we have to define what makes one environment different enough from another to warrant a distinct value of E.
Comment by CHCH — June 6, 2007
This definition is stupid. It contains no insights whatsoever and as already noted, is a regression from defining intelligence. In particular, the notion of “reward” remains undefined. Did I say stupid? I meant —— —— ——. It doesn’t say anything good about your intelligence that you find it “appealing”. Why? Because it’s got greek letters and refers, in a totally useless way I will point out, to other kewl fields of mathematics?
Comment by Richard — June 7, 2007
;-)
I took the liberty to slightly moderate non constructive comments, after all, this is my blog. However, this definition has the ambition to be formal, to avoid human context basis, and it’s the reason why it uses some kind of “univeral” mathematical model.
Reward is defined to stay the most general possible. I think the generality was a goal of the author. It’s right that it requires the definition of the reward for each agent, and it’s not easy, especially for a model of humans. As a human, what is the reward I try to maximise? Money? pleasure? Nb of children? Good food?
But it can be a good model for understanding behaviors of simple animals, or for programming domestic robots (goal: maximize the help you provide to me).
@CHCH: I agree.
This definition isn’t “stupid”, but the pb is difficult.
Another weakness : What if the the reinforcement model isn’t adapted? What if the agent doesn’t get any reward?
Comment by Pierre — June 7, 2007
Pierre: That’s actually an uppercase upsilon, rather than a $\gamma$. :-)
The choice of Turing machine is a subtle issue. In some contexts it doesn’t matter much (for example with Solomonoff induction), but here it matters more. The invariance property from Kolmogorov complexity only affords so much protection. So to some extent U is a free parameter in this definition. There are various possible solutions such as limiting possible U’s to reflect aspects of the structure of our universe, or to condition the complexity on a database of world knowledge (e.g. Wikipedia?).
In some sense complex things have to be less probable simply because there are so many more of them (due to the need to sum to 1 over all possible environments). While a cat might be probable on earth, in a universal sense it’s rather less probable. Universally at least 99.999999% of everything is empty space. Perhaps you don’t really want a truly universal intelligence measure then? Perhaps you want an intelligence measure for things on earth which are about the same size as humans? In this case the measure would need to be conditioned appropriately, such as by conditioning the complexity measure as I mentioned above.
Yes computing this would be a problem. It would have to be estimated. I would actually replace the Kolmogorov measure with a resource bounded complexity measure. I plan on having a go at this sometime in the next year.
Comment by Shane Legg — June 8, 2007
CHCH: The set of environments E is a set of computable measures. Two different programs are two different elements of E and thus it is easy to tell them apart.
Comment by Shane Legg — June 8, 2007
[…] Vía, Yet Another Machine Learning Blog encuentro una nueva definición formal de inteligencia, de esta forma la inteligencia $\gamma$ de un agente (pi) puede expresarse como: […]
Pingback by Inside MetaEmotion » Archivo » Una definición formal (más) de inteligencia — June 8, 2007
Bon Jour Pierre,
I see problematic the definition of “success” in the context of your proposal. What does it mean? How do you measure it? Depending of it, a kokarach would be very intelligent. because as species, they’re present all around, and they’ve been everywhere for billions of years. Doesn’t this affect your definition?
Keep trying,
Raúl
Comment by Raúl — June 8, 2007
Shane : Thank you for your comments. It’s a really general definition. Maybe too general for practical use. P(envi) could be empirical (for instance if you design a robot, you have some knowledge of the env. it’ll see) instead of Kolmogorov-based.
Raul: It’s Shane definition, not mine, but “success” is the expected (future) reward. There is no more constraint of the kind of admissible reward, to stay the most general. Actually one could define strange reward in order to make anthing intelligent; Ex: if the reward is the age, then surely stones ‘ll be really intelligent ;-)
Comment by Pierre — June 8, 2007
Pierre (and Raul):
You can’t just define reward to be the age of the agent. The reward comes from the environment and the set of environments (E) contains all environments that have computable measures. This is not a free parameter. In some of these environments all agents will perform well (such as when the reward is that agent’s age), in others all will perform badly (such as when the reward is always set to 0 no matter what happens). But in others high rewards depend on the agent’s actions, possibly in some very subtle way. It is these environments that separate the smart agents from the dumb ones.
Comment by Shane Legg — June 10, 2007
What strikes me, as a biologist, is how close this definition of “intelligence” is from our concept of “fitness” in evolutionary theory. Fitness is defined (to make it short) as the ability for an organism to survive and reproduce in a given environment. In a biological world, this definition of “intelligence” would then be the ability to survive and reproduce in the highest possible number of environments.
In the artificial intelligence context, “intelligence” would then be the ability for a program (a code?) to persist in a large panel of environments. This reminds me of JM Truong’s hypothesis in his essay (“utterly inhuman”) where he describes the possible emergence of intelligence housed in silicon. His hypothesis is based on the ability for codes to replicate in the interlinked computers of the internet. But this is science-fiction and probably beside the point on this blog…
My point is: the definition given here is about fitness. It is interesting because it can be applied to any entity, not only biological entities, but it is not about intelligence. In my opinion, there can be no intelligence without self-perception.
This was just a remark as I was passing by: I won’t discuss the statistical issues, I’m a biologist, remember?
Comment by Cloé — November 8, 2007